(Toggle Flip-Flop)
RS Flip-Flops
can be combined in a way to produce a circuit that "counts". Remember
the RS Flip-Flop, its output changed to one state with the trigger of
one of its inputs and changed to a different state with the trigger of
the other input. A T Flip Flop alternates output states every time it
receives a pulse on its "clock input" abbreviated as "CLK". The CLK is
an input that keeps the system synchronyzed. In the next section we
will talk about the differences between asynchronys and synchronys
circuits. The clock could be a button that the user presses, every time
he/she wishes to "step" the system, or it could be an automatically
generated signal, also known as a wave or series of pulses. A pulse is
a change from one logical state to the other and back to the original.
It can be brief or long. As far as the counter is concerned, it doesn't
matter. Realistically, however, the pulse can not be too brief. There
is a point where the pulse width is so small, that the transistors
wouldn't be able to switch fast enough. This is one obstacle researches
must continually push through when designing faster and faster
computers.
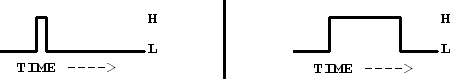
The graph on
the left is a pulse that went high for a relatively short period of
time and the graph on the right lasted for a long period of time.
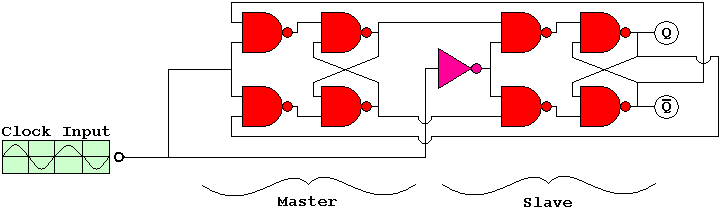
The circuit
above is a T Flip-Flop, a type of master-slave Flip-Flop. Every time
the
input makes a full cycle the Q and 
alternate.
First, lets break apart this into its sub-components:
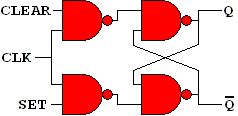This is the original RS
Flip-Flop with gates added to the R and S inputs. It differs from the
original in that it now has a way to be synchronized with other systems
it is involved with. In the old RS Flip-Flop, a change to the R or S
input resulted in an immediate change to that value. The clock added
improved "RS Flip-Flop" doesn't allow the commands to pass through
until the clock goes low. When the clock is high the clear and set
inputs become disconnected from the RS Flip-Flop.
By putting these two blocks together, we can build a T Flip-Flop:
In the T Flip-Flop, on the low clock information is passed from the master section inputs to the master section outputs. Then on the high clock information is transferred to the slave section. This greatly improves the original RS flip-flop by preventing unchecked states and race conditions. Everything happens during a certain "level" of the clock. For this reason it is called a level clocked circuit. One disadvantage to level clocked systems is that input data cannot be reliably changed in between clock cycles. As a general rule all inputs to a level clocked system should be hard wired or driven by something running off of the same clock, such as how the master receive inputs from the slaves outputs in the T Flip-Flop. The other type of clocking, known as edge clocking, has many advantages as well as draw backs. We will discuss it in the next section.
Here is the truth table for the T Flip-Flop
To clear up any confusion you may be having, watch this simulation:
When the clock input goes high, information is passed from the Q outputs back to the "set" and "clear" inputs on the master logic block. Then, when the clock goes low, the information is passed through to the slave and registers on the outputs. The RS Flip-Flops remembers the former state to determine the next state, which is what allows the toggle action.
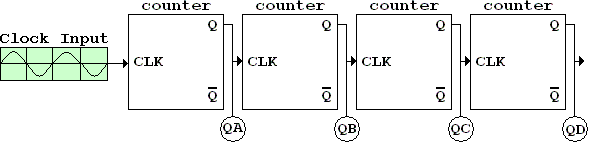
Disregard the value of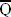 for a
moment, since it is just the opposite of Q. Every time the clock
changes from 0-1 and then back from 1-to-0 (0-1-0), Q alternates to the
other
logical value. So, if Q was previously 1, it now becomes 0. This is a
divide by two binary counter. Two changes on the clock cause one change
on the output. If the output of one of these counter circuits is
connected to another counter circuit the end result would be a divide
by 4 binary counter, or twice as slow as the previous counter.
alternate.
First, lets break apart this into its sub-components: This is the original RS
Flip-Flop with gates added to the R and S inputs. It differs from the
original in that it now has a way to be synchronized with other systems
it is involved with. In the old RS Flip-Flop, a change to the R or S
input resulted in an immediate change to that value. The clock added
improved "RS Flip-Flop" doesn't allow the commands to pass through
until the clock goes low. When the clock is high the clear and set
inputs become disconnected from the RS Flip-Flop. By putting these two blocks together, we can build a T Flip-Flop:
In the T Flip-Flop, on the low clock information is passed from the master section inputs to the master section outputs. Then on the high clock information is transferred to the slave section. This greatly improves the original RS flip-flop by preventing unchecked states and race conditions. Everything happens during a certain "level" of the clock. For this reason it is called a level clocked circuit. One disadvantage to level clocked systems is that input data cannot be reliably changed in between clock cycles. As a general rule all inputs to a level clocked system should be hard wired or driven by something running off of the same clock, such as how the master receive inputs from the slaves outputs in the T Flip-Flop. The other type of clocking, known as edge clocking, has many advantages as well as draw backs. We will discuss it in the next section.
Here is the truth table for the T Flip-Flop
| CLOCK
INPUT |
Q |
|
| 0 |
0 |
1 |
| 1 |
0 |
1 |
| 0 |
1 |
0 |
| 1 |
1 |
0 |
| 0 |
0 |
1 |
To clear up any confusion you may be having, watch this simulation:
When the clock input goes high, information is passed from the Q outputs back to the "set" and "clear" inputs on the master logic block. Then, when the clock goes low, the information is passed through to the slave and registers on the outputs. The RS Flip-Flops remembers the former state to determine the next state, which is what allows the toggle action.
Disregard the value of
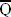for a
moment, since it is just the opposite of Q. Every time the clock
changes from 0-1 and then back from 1-to-0 (0-1-0), Q alternates to the
other
logical value. So, if Q was previously 1, it now becomes 0. This is a
divide by two binary counter. Two changes on the clock cause one change
on the output. If the output of one of these counter circuits is
connected to another counter circuit the end result would be a divide
by 4 binary counter, or twice as slow as the previous counter. The counter
circuit has been replaced by a single "block" with only the inputs and
outputs labeled. By feeding the output of one counter into another, the
original clock speed (cycles per second (Hz) ) is reduced by a factor
of two each time. The end result of this particular example is 16 times
slower than the input frequency. But what does this have to do with
counting?? Keep reading...
The 4 circles above the digit display represent LEDs (when the LEDs are green that means they are on = 1) that are attached (from left to right) to QD,QC,QB,QA on the cascaded counter. The digit display is the decimal conversion of the binary input. Since the 4 bit counter counts from 0-15, the numbers passed 9 cant be displayed in decimal on the digit display. To make a proper 0-9 counter additional logic that checked for the number "10" and then reset the system would need to be added. We will discuss that in a later section.
This is just a glimpse of what flip flops can do. There are many other powerful applications which are found in virtually any digital device. These include, counters, shift registers, memory storage, and synchronizers. We will discuss these in more detail in the upcoming sections
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
0000
Each row represents a
fixed state in between pulses. The top row is the beginning. The second
row is the state after one pulse, the second row after the second
pulse, and so on. The Q values are in reverse order. QA is on the far
right and QD is on the far left, like this:
QD, QC, QB, QA
You may realize
that this pattern exactly matches the binary
number system . By "decoding" this 4-bit value we can
make a simple decimal counter on, perhaps, a 7-segment display.
The 4 circles above the digit display represent LEDs (when the LEDs are green that means they are on = 1) that are attached (from left to right) to QD,QC,QB,QA on the cascaded counter. The digit display is the decimal conversion of the binary input. Since the 4 bit counter counts from 0-15, the numbers passed 9 cant be displayed in decimal on the digit display. To make a proper 0-9 counter additional logic that checked for the number "10" and then reset the system would need to be added. We will discuss that in a later section.
This is just a glimpse of what flip flops can do. There are many other powerful applications which are found in virtually any digital device. These include, counters, shift registers, memory storage, and synchronizers. We will discuss these in more detail in the upcoming sections
